KCF在DSP上的敏捷实践

概要

KCF (Kernelized Correlation Filters)是一种基于模板的目标跟踪算法. 你可以在KCF项目主页找到论文与开源的代码实现.
KCF的实现大致有两类 : 一类是基于Matlab的, 一类是基于OpenCV的C或Python实现. 这两类存在的问题是依赖一些基础库及数据类型, 实际工程需要无依赖的C语言实现.
由于OpenCV库异常复杂, 这篇文章介绍从Matlab到C的敏捷开发. 它采用了Matlab Coder进行快速开发, 思路适用于但不限于KCF算法.
采用了集成测试、单元测试、镜像测试来快速定位Bug.
过程自主原创. 暂时不提供开源代码.

开发

Step 1 Matlab Coder

Matlab Coder的目标是完成由M文件到C文件. 这个功能非常强大, 建议采用较新的Matlab版本, 这里采用的是2018a. Coder需要函数的输入定义, 可以通过编写一个调用此函数的函数, 来自动获取函数输入数据类型.

如果有很多个m文件, 建议全部写到一个m文件中,再进行转换.

容易出现的问题:

1	im = rgb2gray(im);

这种输入im是(width * height *3), 输出im是(width * height)的, C语言无法实现.

可以写成两个变量就好:

1
2
3

im = zeros(width,height,3);
im1 = zeros(width,height);
im1 = rgb2gray(im);

另外条件定义,也无法实现:

1
2
3

if(width>100)
  im = ones(width,height);
end

这种情况,在开头处先进行初始化即可:

im = zeros(width,height);
if(width>100)
  im = ones(width,height);
end

其他一些情况,请参照Matlab Coder的错误提示.

Matlab Coder 存在的问题

有些同学可能会想, 用这个Coder一转, 所有工作就完成了. 然后就可以去😄啦~

但是,总有个但是. Matlab Coder转换出来的代码虽正确，但是存在这样几个问题:

代码冗长,经常有两大长段代码, 差异很小, 但是它没有提取共同项.
代码只实现此次输入会运行到的分支, 其他分支全部删除.
代码会有非常长的数组, 与代码交织在一起.

总结来说, 就是可读性差、可改性差. 如果改一组参数作为输入, 代码大量部分需要修改.

即代码与输入的耦合性太高. 代码模块化混乱. 这样的代码面对改变, 是极其脆弱的.

Step 2 模块化

重构是门艺术. 相对来讲, 本项目的复杂度不算太高 ( C语言1000行以内 ), 在重构之前, 我们必须有集成测试.我们不断地改,改完就把代码扔过去进行集成测试, 以确保我们的代码还没有变质.
测试序列图像

我们采用VOT数据库中的这组视频序列作为输入,记录序列帧的目标跟踪位置. 将目标位置真值、MATLAB计算结果、C计算结果, 绘制成图对比, 相差不是太多的话, 就意味着C版实现仍然工作着.

对于集成测试, 一定要自动化. 要简化到按一次鼠标, 或敲几次键盘就可后台运行测试. 而测试结果是当前时间为名字的图片.我们用shell脚本完成这个测试.

rm ../Debug/*
rm ../output/res.txt
rm test.sh

frame_begin=1;
frame_num=700;

matlab -nodisplay -r "gen_line;quit"
sh test.sh
chmod 777 ../Debug/kcfs
./../Debug/kcfs $frame_begin $frame_num

cd ../auto_test
cd /home/z/github_repo/KCF_detail/matlab_implementation
matlab -nodisplay -r "run_a($frame_begin,$frame_num);quit"

mv pos.txt /home/z/Desktop/c/myfft/myfft/kcfs/output
cd /home/z/Desktop/c/myfft/myfft/kcfs/auto_test
matlab -nodisplay -r "add_rect($frame_begin,$frame_num);quit"

frame_begin, frame_num是函数的输入参数, 即从第几帧开始与总共多少帧.

第三段调用gen_line脚本, 生成gcc控制参数,之后运行C实现.

第四段调用run_a脚本,运行Matlab实现.

第五段对跟踪结果进行处理, 叠加矩形框进行观察及跟踪结果对比图绘制并保存.

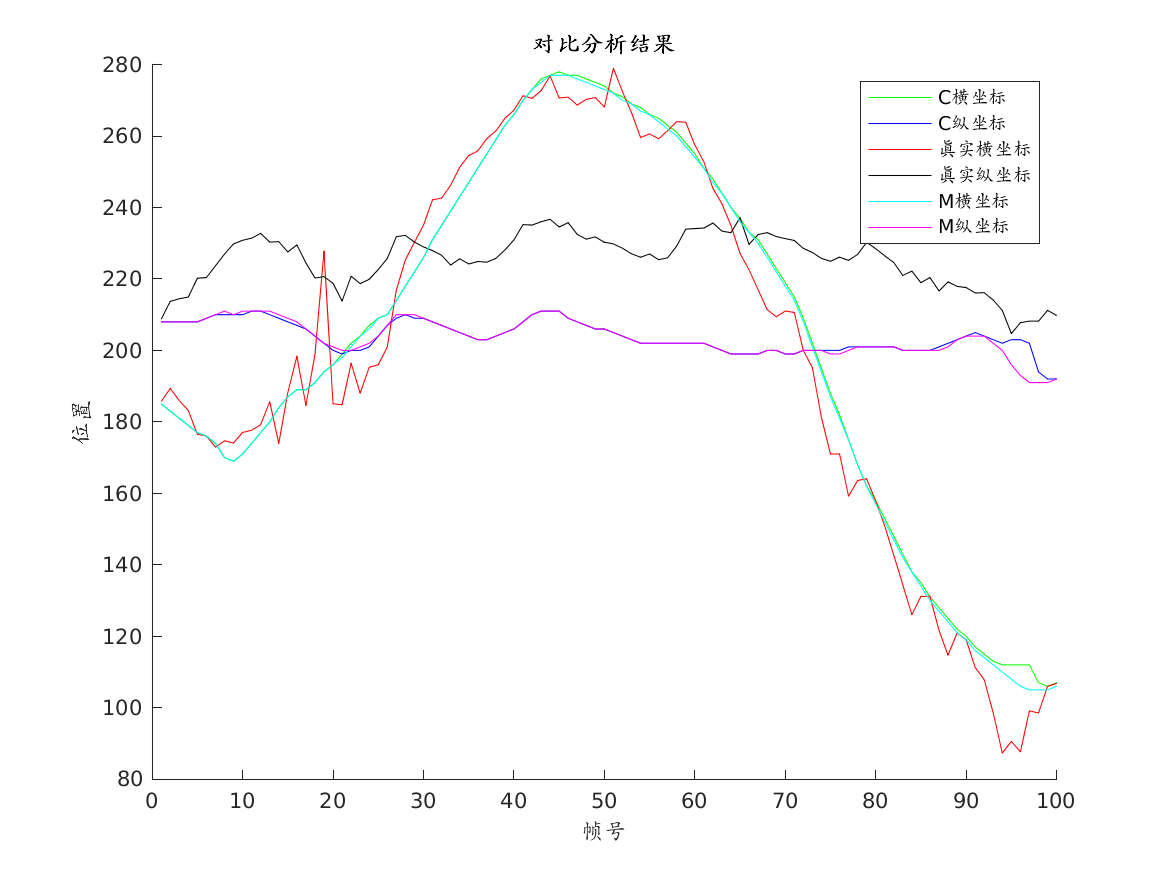
集成测试对比结果

模块化细节

需要一个复数的数据结构，自己实现，不要用很大的系统头文件．

typedef struct
{
  double re;
  double im;
}creal_T1;

FFT的实现

void fft(creal_T1 vector[],int N)
{
  int dig,k,n,m,i,j1,dist,idx,idx1,r;
  creal_T1 coef,tmp,mul_res;

  change(N,vector);
  dig = 0;
  k = N;
  while(k > 1){
      dig = dig + 1;
      k = k / 2;
  }
  n = N / 2;
  for(m=1;m<=dig;m++)
  {
      dist = pow(2, (m - 1) );
      idx = 1;
      for(i = 1;i<=n;i++){
        idx1 = idx;
        for(j1 = 1; j1 <= (N / (2 * n)); j1++){
            r = (idx - 1) * pow(2, (dig - m));
            if(N==256)
            {
              coef.re = cos_256[(r % N) / N];
              coef.im = -sin_256[(r % N) / N];
            }
            else if(N==128)
            {
              coef.re = cos_128[(r % N) / N];
              coef.im = -sin_128[(r % N) / N];
            }
            else
            {
                coef.re = cos(2 * M_PI * r / N);
                coef.im = -sin(2 * M_PI * r / N);
            }
            coef.re = cos(2 * M_PI * r / N);
            coef.im = -sin(2 * M_PI * r / N);
            
            tmp.re = vector[idx-1].re;
            tmp.im  = vector[idx-1].im;
            mul(vector[idx + dist-1], coef, &mul_res);
            add(tmp, mul_res, &vector[idx-1]);
            sub(tmp, mul_res, &vector[idx + dist-1]);
            idx = idx + 1;
        }
        idx = idx1 + 2 * dist;
    }
    n = n / 2;
  }
}

这里要求点数必须是２的整数次幂，相当于搜索范围可以弹性调整一下．Matlab的FFT在非２的整数次幂时，进行了DFT运算. 这里和Matlab不一致．为了加快FFT的速度，可以优化成用查表法实现．

FFT2的实现

void fft2(creal_T1 vector[],creal_T1 vector1[],int M,int N)
{
   creal_T1 hang[N];
   creal_T1 lie[M];
   int i,j;

   for(j=1;j<=N;j++){
     for(i=1;i<=M;i++){
       lie[i-1].re = vector[ ((j-1)+ (i-1)*N) ].re;
       lie[i-1].im = vector[ ((j-1)+ (i-1)*N) ].im;
     }
     fft(lie,M);
     for(i=1;i<=M;i++){
       vector[ ((j-1)+ (i-1)*N) ].re = lie[i-1].re;
       vector[ ((j-1)+ (i-1)*N) ].im = lie[i-1].im;
     }
   }
  for(i=1;i<=M;i++){
    for(j=1;j<=N;j++){
      hang[j-1].re =vector[ (j-1)+ (i-1)*N ].re;
      hang[j-1].im =vector[ (j-1)+ (i-1)*N ].im;
    }
    fft(hang,N);
    for(j=1;j<=N;j++){
      vector[ (j-1)+ (i-1)*N ].re = hang[j-1].re;
      vector[ (j-1)+ (i-1)*N ].im  = hang[j-1].im;
    }
  }

  for(i=1;i<=M;i++){
    for(j=1;j<=N;j++){
      vector1[ (j-1)+ (i-1)*N ].re = vector[ (j-1)+ (i-1)*N ].re;
      vector1[ (j-1)+ (i-1)*N ].im  = vector[ (j-1)+ (i-1)*N ].im;
    }
  }
}

二维FFT就是将图像按每行进行一遍FFT后，在按每列进行一遍FFT.

kcf C实现汇总

文件名称		行数	描述
.c	main.c	261	主程序
	circshift.c	30	循环移位
	conj_f.c	11	取共轭
	data_input.c	17	数据读入
	div_f.c	16	复数矩阵除法
	exp.c	25	矩阵e指数次幂计算
	mul_f.c	16	矩阵复数乘法
	myfft.c	215	fft相关
	ndgrid.c	18	N维网络插值
	power.c	9	矩阵平方计算
.ｈ	p_def.h	35	参数预定义

测试

单元测试

随着代码复杂度的提升，对于bug定位及代码质量保证提出挑战．模块化的代码就是一层一层搭积木的过程，确保每一层可靠，非常关键．
对于Ｃ语言而言，传统的单元测试是在Ｃ平台构建测试激励，与预想进行比对．考虑到Ｃ语言是一种抽象层次较低的语言，在Ｃ平台下进行测试费时（代码写的慢）费力（代码写的长）．这里才用Matlab平台进行测试，而Ｃ语言的代码，通过mex函数，转换成ＭATLAB可运行的mexw64（64位机器下）．

我们以c_exp这一复数矩阵指数次幂计算为例，ｃ语言函数如下：

void c_exp(creal_T1 x[box_p])
{
  int k;
  double x_re;
  double r;
  for (k = 0; k < box_p; k++) {
    r = exp(x[k].re / 2.0);
    x_re = r * (r * cos(x[k].im));
    r *= r * sin(x[k].im);
    x[k].re = x_re;
    x[k].im = r;
  }
}

对应编写的mex函数如下

#include "mex.h"
#include "p_def.h"
#include <math.h>

void c_exp(creal_T1 x[box_p])
{
  int k;
  double x_re;
  double r;
  for (k = 0; k < box_p; k++) {
    r = exp(x[k].re / 2.0);
    x_re = r * (r * cos(x[k].im));
    r *= r * sin(x[k].im);
    x[k].re = x_re;
    x[k].im = r;
  }
}
void mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[]){
    creal_T1 *input1;
    double* input1_re;double* input1_im;
    double* out_re;   double* out_im;
    int RowA,ColA,i;
    if(nlhs != 1){
       mexErrMsgTxt("One output required.");
    }
    else if(nrhs !=1){
        mexErrMsgTxt("One input required.");
    }
    RowA = mxGetM(prhs[0]);
    ColA = mxGetN(prhs[0]);
    input1_re = mxGetPr(prhs[0]);
    input1_im = mxGetPi(prhs[0]);
    input1 = malloc(sizeof(creal_T1)*RowA*ColA);
    for(i=0;i<RowA*ColA;i++)
    {
      input1[i].re = input1_re[i];
      input1[i].im = input1_im[i];
    }
    plhs[0] = mxCreateDoubleMatrix(RowA,ColA,mxCOMPLEX);
    out_re = mxGetPr(plhs[0]);
    out_im = mxGetPi(plhs[0]);
    c_exp(input1);
    for(i=0;i<RowA*ColA;i++)
    {
      out_re[i] = input1[i].re;
      out_im[i] = input1[i].im;
    }
    free(input1);
}

通常的mex函数的写法，网上介绍的比较多，这里只重点介绍数据类型为复数的情形．

通过mxGetPr和mxGetPi分别获取输入的实部和虚部．用mxCreateDoubleMatrix创建复数矩阵．

mex函数主要只是要完成Ｃ语言与m语言输入输出的转换和绑定，应该说是比较简单的．

在此基础上，我们看一下单元测试的过程：主要由atest与stest两部分组成．

clc; close all;clear all;

p1 = mfilename('fullpath');
j=findstr(p1,'/');
p1=p1(1:j(end));
cd(p1);
addpath('../');


% testcase1  2*2
input1 = zeros(2,2);
input1 = [1+i,2-i;3+i,4-i];
stest_c_exp(input1,1);


% testcase2  256*128
input1 = zeros(256,128);
for j=1:256
  for k=1:128
    input1(j,k) = j*0.1+2i;
  end
end

stest_c_exp(input1,2);

%testcase3  1024*1024
input1 = zeros(1024,1024);

for j=1:1024
  for k=1:1024
    input1(j,k) = j*0.01+3i;
  end
end

stest_c_exp(input1,3);

atest主要完成测试用例的生成，并调用stest进行测试．

function stest_c_exp(input1,seq)

  fid = fopen(['c_exp_' num2str(seq) '.txt'],'r');
  A = fscanf(fid,'%f,');

  gt0                 = A(1);
  gt1                 = A(2);
  gt2                 = A(3);
  gt3                 = A(4);
  padding             = A(5);
  ifr                 = A(6);
  cell_size           = A(7);
  lambda              = A(8);
  sigma               = A(9);
  output_sigma_factor = A(10);
  im_w                = A(11);
  im_h                = A(12);
  box_w               = A(13);
  box_h               = A(14);
  box_p               = A(15);

  if(exist('p_def.h'))
    delete('p_def.h');
  end
  create('p_def.h', A);
  delete('mex_c_exp.mexa64');
  mex('mex_c_exp.c');

  output1 = exp(input1);
  output2 = mex_c_exp(input1);

  res = compare(output1,output2);

  fprintf('%s',"c_exp's testcase ");
  fprintf('%d',uint8(seq));
  if(res == 1)
    fprintf('%s\n'," success");
  else
    fprintf('%s\n'," fail");
  end

stest完成某组参数下的Ｃ实现及Ｍatlab实现对比．如果误差足够小，打印success.否则打印 fail.

镜像测试

在进行完所有的单元测试，均通过的前提下，程序还是不正确（集成测试无法通过）．那就要靠强大的镜像测试（名字自定义的）．所谓镜像测试，就是跑一步m, 跑一步Ｃ，然后对比结果．main的每一行都进行对照，直到能够找到问题所在．镜像测试看起来是这样：


pos1= [gt1 + floor(gt3/2)  gt0 + floor(gt2/2)];
pos2= [gt1 + floor(gt3/2)  gt0 + floor(gt2/2)];

output_sigma = sqrt(gt2*gt3) * output_sigma_factor / cell_size;

labels1 = gaussian_shaped_labels(output_sigma, ceil(window_sz / cell_size));
labels2 = mex_gaussian_shaped_labels(gauss);
step_i = 1;
res = compare(labels1,labels2);
if(res == 1)
  fprintf('%s %d %s\n',"step",step_i,"success");
else
  fprintf('%s %d %s\n',"step",step_i,"fail");
end
step_i = step_i + 1;

 yf1 = fft2(labels1);
 yf2 = mex_fft2_d(labels2,box_w,box_h);
 res = compare(yf1,yf2);
 if(res == 1)
   fprintf('%s %d %s\n',"step",step_i,"success");
 else
   fprintf('%s %d %s\n',"step",step_i,"fail");
 end
 step_i = step_i + 1;

后续

完成完整的KCF (Hog特征)．
优化Ｃ版KCF的速度．
在C6678上进行真实测试．

总结

这篇文章主要介绍了KCF由Ｍ到Ｃ的开发过程．采用了测试与开发并重的敏捷实践．提出的方法具有普适性：基于Matlab Coder的使用，完成了ｍ设计开发，Ｃ运行应用的设想．在开发者的时间越来越宝贵的今天，让开发者不再纠结于Ｃ语言的disgusting的细节，而又能享受到Ｃ语言的跨平台、高速度、适用于嵌入式的优点，是很有必要的。